Pytorch ——基础指北_柒(使用线性网络实现数字识别)

[TOC]
软件环境:
- pytorch 1.10
- pycharm
使用MNIST构建自己的数据集
详细的可以参考:
这里不再赘述,直接放上代码来说:
def MNIST_create_dataloader(train=True):
transforms_fn = Compose([ToTensor(), Normalize(mean=0.1307, std=0.3081)])
#这里是对数据集进行预处理,将普通图像转换成pytorch支持的图像,并对数据分布进行调整
MNIST_dataset = MNIST(root="./data", train=train, download=True, transform=transforms_fn)
#导入官方的数据集,并转化成Dataset类
MNIST_dataloader = DataLoader(dataset=MNIST_dataset, batch_size=batch_size, drop_last=True, shuffle=True, )
#对Dataset类处理转化成DataLoader类
return MNIST_dataloader
这样一个MNIST数据就完成了预处理等操作,很快就能构建好。
如何构建模型?
基础知识参考给于的链接。
我们使用nn.Module类来构建自己的模型,我们目前需要一个简单的模型层数不需要太多,只使用全连接层即可,因为是一个分类模型,所以需要通过激活函数来实现对0~9的分类,你可以注意到他并不是简单的二分类而是10分类模型,这样的话sigmod激活函数就没有办法使用了,我们这里就要使用relu来作为激活函数,最后配合权重loss实现10分类。整体网阔结构框架如下:

下面就来讲解如何实现这个小网络。
图像的扁平化处理
首先我们关注网络开始的部分:
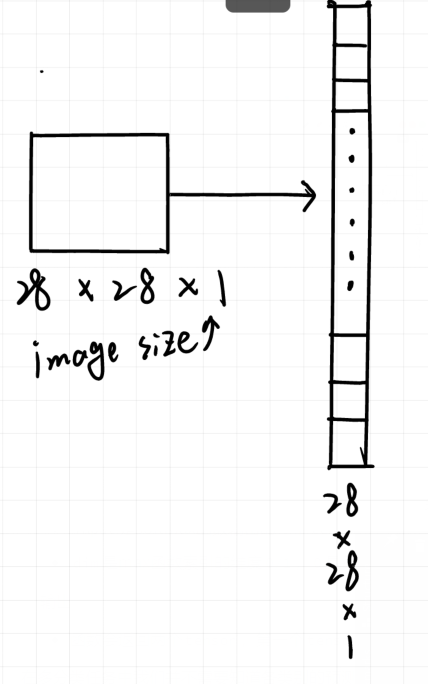
在构建完成数据集以后,我们可以看到数据在每个batch的时候,其实并不是一张图片,而是batch_size * image_size(这里的image_size就是28 * 28 * 1,单个图像包含的像素数量)见下图,网络在训练的时候我们并不是每次只送进去一张图像而是送进去多张图像,为了构建模型就要考虑到这些问题,我需要将每个batch内的图像再分开送入吗?当然不用!pytorch内置的全连接层只需要我们输入特征数量即可无需考虑batch_size,这为我们构建模型提供了很大的方便。
batch为1415的两张图片(两张图片代表的分别为1和0)和它们的的label((tensor([1, 0]))转化成tensor的样子:
1415 [tensor([[[[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
...,
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242]]],
[[[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
...,
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242],
[-0.4242, -0.4242, -0.4242, ..., -0.4242, -0.4242, -0.4242]]]]), tensor([1, 0])]
首先对输入图像从二维进行扁平化处理:
所谓扁平化实际上就是把数据从2维降维到1维度,方便运算。
至于这里为什么要1维,我们先保留以后再进行讨论:
这里先介绍方法:
def forward(self, input):
x = input.view(-1, 1 * 28 * 28)
这里的foward方法就是前向传播的方法,首先要知道每一个batch内的数据是这样的:
[batch_size * [image_width * [image_height*[channel_num]]]]
可以看到实际上是四层的数据,也就是四维【图片3维+batch维度(有几张图片)】
pytorch对于其扁平化调用view方法即可,view方法及原理使用可参见:
注意这里不能调用permute方法,而应该是view方法,注意区别这两个的方法。
转化后数据就转变成二维的形状:
[batch_size,image_size]。
接下来就是如何构造第一个输入全连接层了。
构造输入全连接层

构建输入层,将数据变形从28*28个像素提取出来28个特征,这是输入层的目的。
但是为什么全连接层能将28*28的数据转化成28呢?全连接层的本质是什么呢?
看下边一张图:

对于上图全连接层的描述可以变换成一个矩阵,图中左侧矩阵代表着每个连线上的权重参数W,右侧矩阵就是输入数据(已经一维化)。
对于目前的网络可以看如下解释:
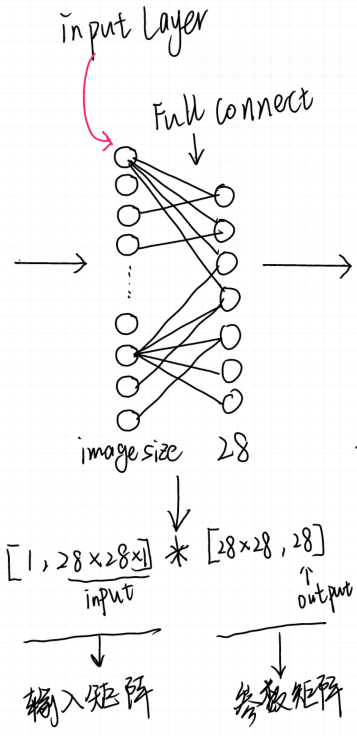
输入数据矩阵:
[1,28 * 28* 1]
参数矩阵:
[28 * 28 ,28]
进行矩阵相乘以后就变成了 如下的[28 ,1 ]的向量。
那么如何在代码中实现呢?可以看到我先继承了nn.Module类并调用了父类的初始化,然后在模型中初始化了一个输入特征为:1* 28 * 28(扁平化化后的图片) ,输出特征为28的线性全连接层。
class Mymodule(nn.Module):
def __init__(self):
super(Mymodule, self).__init__()
self.fc1 = nn.Linear(1 * 28 * 28, 28)#初始化一个全连接层
在前向传播方法中 如何使用设定好的全连接层呢?
很简单,调用你的全连接层传入输入参数即可:
def forward(self, input):
x = input.view(-1, 1 * 28 * 28)
x = self.fc1(x)#调用全连接层
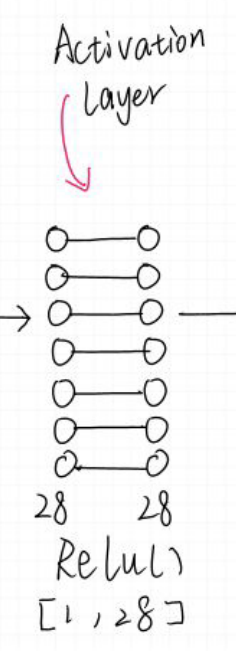
完成了输入特征的提取就来到了激活函数层。
我们在这里选择了Relu作为激活函数,激活函数的作用很多,增加非线性分割能力,缓解梯度消失,增加收敛速度等。
RELU则是图像处理常用的函数,这里不再赘述,详情可看:
这里只讨论用法:
import torch.nn.functional as F
class Mymodule(nn.Module):
def __init__(self):
super(Mymodule, self).__init__()
self.fc1 = nn.Linear(1 * 28 * 28, 28)
def forward(self, input):
x = input.view(-1, 1 * 28 * 28)
x = self.fc1(x)
x = F.leaky_relu_(x)
使用方法很简单直接调用即可:
x = F.leaky_relu_(x)
这样在前向传播的时候就相当于添加了一层激活函数层来进行运算。

激活后就要考虑如何构造输出层。
输出层的构造
前面我们讲到过对于输出层我们常用的loss函数就有两种:
$$
\begin{array}{ll}
\operatorname{loss}=\left(Y_{p r e d i c t}-Y_{\text {true }}\right)^{2} & \text { (回归损失) } \
\operatorname{loss}=Y_{\text {true }} \cdot \log \left(Y_{\text {predict }}\right) & \text { (分类损失) }
\end{array}
$$
我们需要明确,当前我们手写字体识别的问题是一个多分类的问题,所谓多分类对比的是之前学习的2分类,我们在逻辑回归中,我们使用sigmoid进行计算对数似然损失,来定义我们的2分类的损失。多分类和2分类中唯一的区别是我们不能够再使用sigmoid函数来计算当前样本属于某个类别的概率,而应该使用softmax函数。softmax和sigmoid的区别在于我们需要去计算样本属于每个类别的概率,需要计算多次,而sigmoid只需要计算一次
softmax的公式如下:
$$
\sigma(z)j = \frac{e^{z_j}}{\sum^K{k=1}e^{z_K}} ,j=1 \cdots k
$$
其中z代表的就是上一层的输出结果,本质上就是对其求指数化后再进行求和和总占比,这里不再赘述,输出的结果就是概率的大小。
这里我们不急着讲解怎么用,我们再来介绍一个内容:
交叉熵损失函数
$$
\begin{equation}
H(y, y_p)=-\sum_{x}(y \log y_p)
\end{equation}
$$
其中y_p为预测结果,y为正确结果。如果你对他的求导感兴趣可以参考:交叉熵损失函数
为什么要把概率输出和损失函数一起介绍呢?
因为在Pytorch中有一个很方便的API可以直接构造一层softmax函数+交叉熵损失函数,方便我们训练。
这个API就是 :nn.CrossEntropyLoss()
它的使用很简单,只需要实例化这个对象然后传入预测结果与真实目标值即可:
loss_fun = nn.CrossEntropyLoss()
loss = loss_fun(output, target.to(device))
当然值得注意的是loss函数并不是模型的一部分,所以loss的创建不要在nn.Module类下,最后完整的模型如下:
class Mymodule(nn.Module):
def __init__(self):
super(Mymodule, self).__init__()
self.fc1 = nn.Linear(1 * 28 * 28, 28)
self.fc2 = nn.Linear(28, 10)
def forward(self, input):
x = input.view(-1, 1 * 28 * 28)
x = self.fc1(x)
x = F.leaky_relu_(x)
x = self.fc2(x)
return x
你会注意到这里多了一个线性层:
x = self.fc2(x)
这个线性层的是这样的:
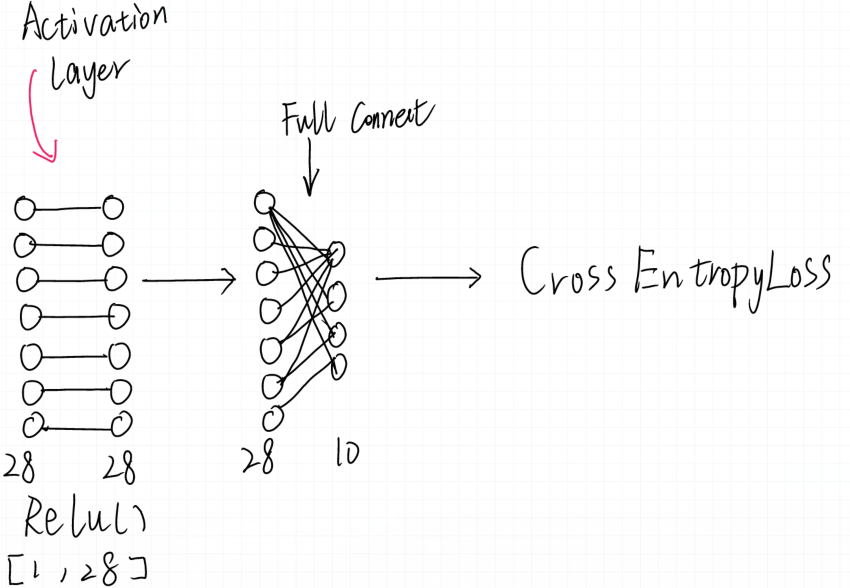
你可以看到他前边有28个节点,后一层只有10个节点,你应该能想到,其实就是对28个特征再次进行变换将它压缩到10个特征,这十个就分别对应了需要识别的10个数字,最后配合交叉熵来进行训练,更新权重信息完成网络。
完整的训练代码如下:
batch_size = 2 #每批两个图像
device = torch.device("cpu")#调用cpu作为设备使用
def train(epoch):
mode = True
mymodule_net.to(device)
for times in range(epoch):
mydataloader = MNIST_create_dataloader(train=mode)
for index, (input, target) in enumerate(mydataloader):
myopt.zero_grad()#清零梯度信息
output = mymodule_net(input.to(device))#调用模型前向传播
loss_fun = nn.CrossEntropyLoss()#Loss函数初始化
loss = loss_fun(output, target.to(device))#计算loss
loss.backward()#反向传播计算梯度
myopt.step()#更新参数
if index % 100 == 0:#每一百次训练输出一下信息
print(times, index, loss.item())#训练次数,训练进度,loss信息
最后输出信息如下:
9 28700 1.7881361600302625e-06
9 28800 0.001552493660710752
9 28900 8.34461025078781e-06
9 29000 0.0030884044244885445
9 29100 0.0003478508733678609
9 29200 1.7881390590446244e-07
9 29300 1.7881390590446244e-07
9 29400 0.0
9 29500 0.12013460695743561
9 29600 1.0683552026748657
9 29700 0.00016692475765012205
9 29800 0.0013533380115404725
9 29900 2.264973545607063e-06
可以看到第十次训练的时候,loss已经非常低了,说明还是比较成功的。完整代码请扫描二维码下载,请给个star!。