Pytorch ——基础指北_贰

软件环境:
- pytorch 1.10
- pycharm
[TOC]
基础知识:
要想训练一个网络,对于梯度的理解是必不可少的,下面首先介绍梯度的一些基础概念。
0、方向余弦与向量单位化
方向余弦是一个在向量中很常见的概念,它用来标定某一个向量的方向,说起来可能会一头雾水,不过没关系,我们使用画图来理解一下。
举个例子,如下图有一个坐标系xoy,其效果如下所示:
其中包含了一个向量$\overrightarrow{l}$ ,向量的坐标为:$(a,b)$
那么上文中的向量就满足如下式子:
$$
(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}})
$$
上文的式子实际上就是对向量进行单位化,此时新产生的向量,实际上就是我们常说的方向向量。
方向向量实际上还可以再优化一下,我们看到图上还有两个标明的角分别是$\alpha和\beta$,这两者的关系就不再多说,他们呢一对互余的角度,满足的条件就是相加等于90度。
此时我们就可以将这个式子转化成这样的形式:
$$
\frac{a}{\sqrt{a^2+b^2}} = \cos{\alpha}
$$
同理也有:
$$
\frac{b}{\sqrt{a^2+b^2}} = \cos{\beta}
$$
这样方向的向量的表达式,就可以写为:
$$
(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}) =(\cos{\alpha},sin{\alpha})
$$
实际因为角度互余上可以化为:
$$
(cos{\alpha},cos{\beta})
$$
1、多元函数求偏导
一元函数,即有一个自变量。类似$f(x)$
多元函数,即有多个自变量。类似$f(x,y,z),三个自变量x,y,z$
多元函数求偏导过程中:对某一个自变量求导,其他自变量当做常量即可
例1:

例2:

例3:

练习:
已知$J(a,b,c) = 3(a+bc),令u=a+v,v = bc$,求a,b,c各自的偏导数。

2、方向导数:
简单地说方向导数形容的是满足某个关系下(Y=KX+B),对于各个方向上本关系数值变化率(Y的变化率)的量化表达式。
数学推导,可参考如下文章。但是我读完以后还是没办法一下就理解,它实际上不应该是一个这么难理解的内容,我们反过来想一想,能不能从前面的基础构建出来方向导数到底是什么。
从二维、三维入手
在二维关系中Y=KX+B中我们不太好理解什么是方向导数,我们知道对于一个函数来说,$y=kx+b$的导数实际上是这样的:
对于函数的某一点,导数等于切线在该点的斜率,他是一个极限概念。我们不妨这样来理解这个极限的过程:
下图是某个函数,其中包含三个点如下所示:
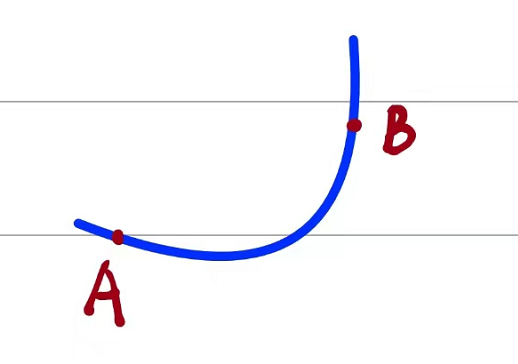
其中A、B是函数上随机的两个点。其中A、B两点满足如下:
$$
A= (x_0,f(x_0))\
B= (x_0+\Delta x,f(x_0+\Delta))
$$
然后AB两点相连接,形成一个割线,割线的斜率满足如下条件:
$$
k_{AB} = \frac{f(x_0+\Delta x) - f(x_0)}{(x_0+\Delta x) - x_0} = \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}
$$
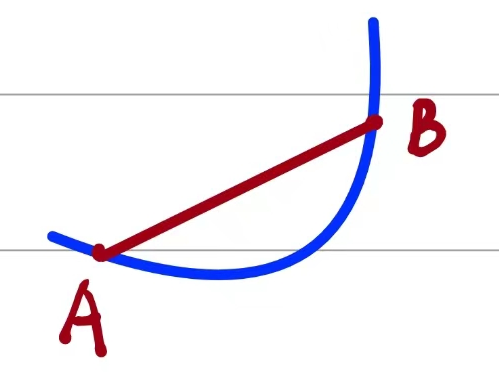
当有如下情况的时候,就会产生切线和导数:
当B无限趋近于A的时候,即$\Delta x$无限趋近于0的时候,割线AB就会转化为切线,如下所示:
满足的数学关系如下:
$$
k_{ab} = \varliminf_{\Delta x \to 0} \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}
$$
而我们知道切线的斜率就是导数的值,这是在二维的情况下。
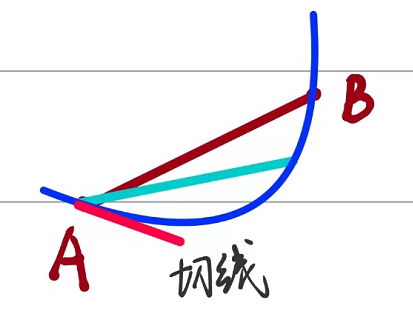
三维的方向导数
在二维的情况我们已经很了解了,我们来推广到到三维的情况下来试一试,举个例子:
我们先来下一个定义:
一般情况下的三位函数的方向导数实际上是平面XOY上一点$(x,y)$在三维函数的值$f(x,y)$,和其所代表的一点$(x,y,f(x,y))$以向量l的方向向量为切面构成的曲线上(点(x,y))的一条切线的值。
说起来很抽象,我们举个例子就好理解一点了:
其中三维函数圆形抛物面大致如下:
$$
Z = x^2+y^2
$$
如图所示:
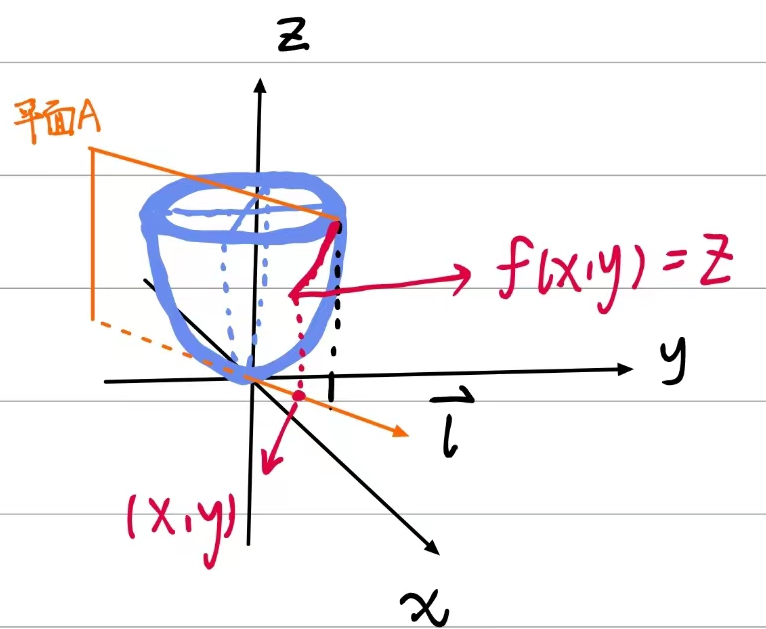
图看起来很很复杂不过没关系,我们依靠颜色来分辨一下:
红色包含两部分内容:分别是在xy平面的点$(x,y)$和切面构成的曲线。
橙色包含两部分内容:$\overrightarrow{l}$ 是 $XOY$ 平面(笛卡尔坐标系)上以 $P(X_0,Y_0)$为始点的一条射线,$e_l = ( \cos \alpha , \cos \beta)$ 是与 L 同方向的单位向量。同时还包含一个由其方向向量构建出来的平面A。
蓝色部分包含一个内容:就是函数Z。
我们来解析一下这分别什么意思
当存在一个点c从点(x,y)出发沿着方向向量变化$t$的时候,其坐标满足如下:
$$
C = (x+tcos{\alpha},y+tcos{\beta}) (其中角度和上文中的是一样意义)
$$
这时候c点实际上就是黑色虚线在l上的点。这时候这个在向量上的变化轨迹就是一段向量,他的方向和l向量的方向向量是一样的,并且在函数上映射了一段曲线,如红色部分曲线所示,我们针对这一种曲线来考虑一种特殊情况,当满足这个条件的时候,曲线会如何变化?
没错就是上文中二维的情况:

结果是一模一样的,只不过这里的切线是对应的在曲线上的切线,我们这里就引出方向导数的定义如下:
$$
\left. \frac{\partial f}{\partial l} \right|_ {\left(x_{0}, y_{0}\right)} = \lim_{t \rightarrow 0^{+}} \frac{f\left(x_{0} + t \cos \alpha, y_{0} + t \cos \beta \right) - f\left(x_{0}, y_{0}\right)}{t}
$$
从方向导数的定义可知,方向导数:$ \left. \frac{\partial f}{\partial l}\right|_ {\left(x_{0}, y_{0}\right)} $就是函数 $ f(x, y) 在点 P_{0}(x_{0}, y_{0}) $处沿方向 ( l ) 的变化率。
定理:
如果函数$f(x, y)$ 在点$P_{0}\left(x_{0}, y_{0}\right)$可微分,那么函数在该点沿任一方向 的方向导数存在,且有 :
$$
\left.\frac{\partial f}{\partial l}\right|_ {\left(x_{0}, y_{0}\right)}=f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta
$$
注意里面为偏导 实际上就分解成了X Y轴上函数变化率。
其中, $\cos \alpha \text { 和 } \cos \beta$是向量$l$ 的方向余弦。
这里再说明一下方向导数和偏导数有什么区别呢?
偏导数实际上方向导数的特例,当向量取x的正轴的时候,此时方向导数就转变为了对于x的偏导数,推导如下:
$$
\left.\frac{\partial f}{\partial l}\right|_ {\left(x_{0}, y_{0}\right)} = \lim_ {t \rightarrow 0^{+}} \frac{f\left(x_{0}+t \cos \alpha, y _{0}\right)-f\left(x _{0}, y _{0}\right)}{t}
$$
如果你仔细看就会发现实际上这里的定义就是偏导数的定义,也就说是方向导数的一种情况。
其次再说明一下,这个式子的意义在哪里:
$$
\left.\frac{\partial f}{\partial l}\right|_ {\left(x_{0}, y_{0}\right)}=f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta
$$
实际上,我们用来计算方向导数的时候就是使用这个式子,这个式子就是将对应的方向向量分解为x轴和y轴的方向余弦来进行计算,也就说方向向量实际上是由x轴和y轴的方向余弦构成的。
还有就是对于用同一个点,方向向量不同所构成的方向导数大小也不同,但是这些方向导数的方向始终会在一个平面内,这个平面就是这个点的切平面!
3、梯度:
梯度是方向导数的特例:
$$
\operatorname{gradf}(x, y) = \frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y} \vec{j}
$$
已知在某个点有方向导数存在下列关系:
$$
\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x} \cos \varphi + \frac{\partial f}{\partial y} \sin \varphi = \left\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right\} \cdot \{\cos \varphi, \sin \varphi\}
$$
在方向 L上满足如下单位向量:
$$
\overrightarrow{\boldsymbol{e}}=\cos \varphi \overrightarrow { \boldsymbol{i}}+\sin \varphi \overrightarrow{ \vec{j} }
$$
则方向导数可转化成如下:
$$
\frac{\partial f}{\partial l}= \begin{equation}\operatorname{gradf}(x, y)\end{equation} * \overrightarrow{\boldsymbol{e}}
$$
点积就相当于做一个投影,方向导数 和 梯度 之间保持一定的夹角(做点积)来构成各个方向上的方向导数。什么时候方向向量最大呢?
很容易想到不存在夹角的时候就可以满足,因为此时点积最大即满足下列条件:
$$
\begin{equation}
\text { 只有当 } \cos (\operatorname{grad} f(x, y), \vec{e})=1 , \frac{\partial f}{\partial l} \text { 才有最大值。 }
\end{equation}
$$
函数在某点的梯度是个向量,他的方向与方向导数最大值取值的方向一致,其大小正好是最大的方向导数。
梯度概念理解:如下图所示,在p点放一个热源的等温线,则热源的辐射从里到外为10°、20°、30°、40°,若一个小蚂蚁在o点,要最快逃离热源,应该往oj方向逃离,若往om方向逃离则热源的变化率为0,即一直都是20°,也就是说蚂蚁一旦确定了某个逃离方向(0°,90°)方向角逃离,只要一直沿着该方向一直走,就是最快的热源降低的方向
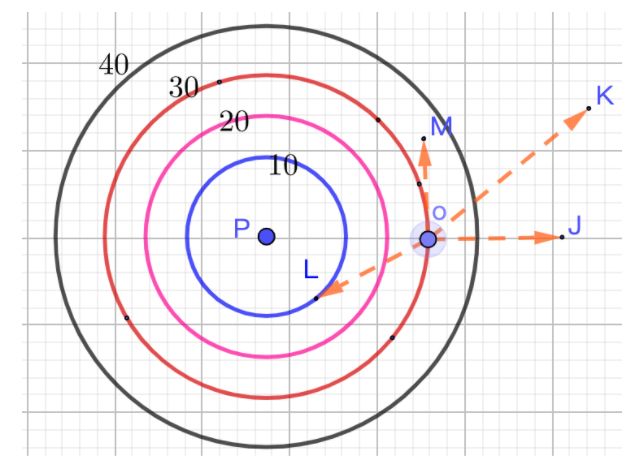
对于一维线性函数其导数就是梯度。
各种函数的梯度与导数的关系:
更详细的解释可以参考参考文献链接。
Tensor的梯度与反向传播
回顾机器学习
收集数据$x$ ,构建机器学习模型$f$,得到$f(x,w) = Y_{predict}$
如何判断模型的好坏?判断模型好坏的方法:
$$
\begin{array}{ll}
\operatorname{loss}=\left(Y_{p r e d i c t}-Y_{\text {true }}\right)^{2} & \text { (回归损失) } \
\operatorname{loss}=Y_{\text {true }} \cdot \log \left(Y_{\text {predict }}\right) & \text { (分类损失) }
\end{array}
$$
通过最终 $loss$ 的输出,来反向传播计算梯度大小进而调整参数的大小实现最优解。
当 $loss$ 满足如图时候
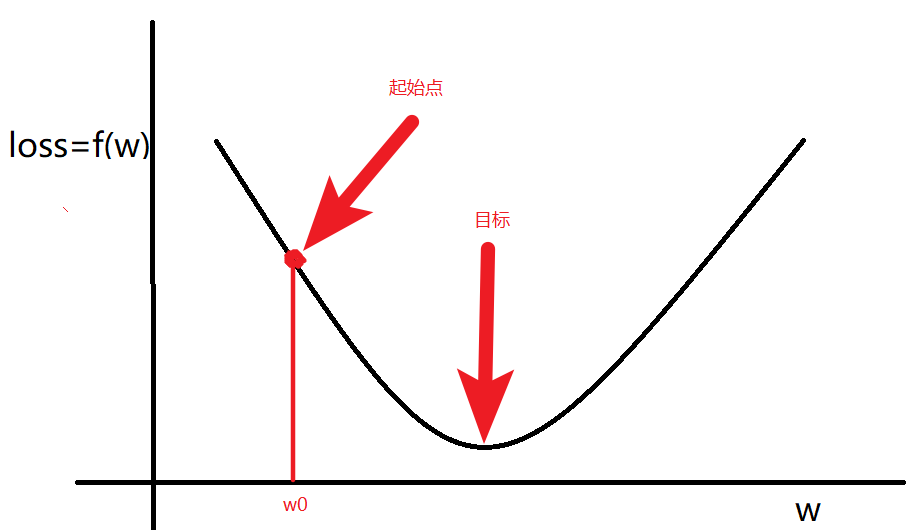
计算出来梯度以后:朝着梯度变化的方向运算,随机选择一个起始点$w_0$,通过调整$w_0$,让 $loss$ 函数取到最小值。

$w$的更新方法:
- 计算$w$的梯度(导数)
$$
\nabla w = \frac{f(w+0.000001)-f(w-0.000001)}{2*0.000001}
$$
- 更新$w$
$$
w = w - \alpha \nabla w
$$
其中:
- $\nabla w <0 $ ,意味着w将增大
- $\nabla w >0 $ ,意味着w将减小
总结:梯度就是多元函数参数的变化趋势(参数学习的方向),只有一个自变量时称为导数,拥有多个时称为偏导数。
反向传播?
计算图
为了方便描述,通过图的方式来描述函数。
$J(a,b,c) = 3(a+bc),令u=a+v,v = bc$,把它绘制成计算图可以表示为:
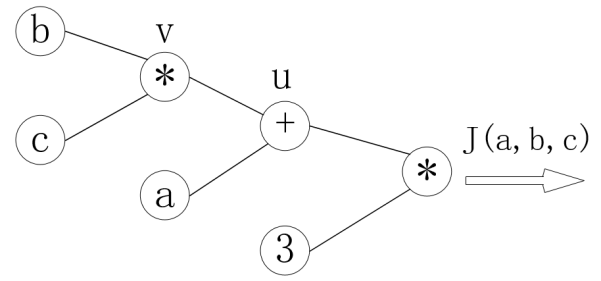
对每个节点求偏导可有:

反向传播的过程就是一个上图的从右往左的过程,自变量$a,b,c$各自的偏导就是连线上的梯度的乘积:
$$
\begin{align*}
\frac{dJ}{da} &= 3 \times 1 \
\frac{dJ}{db} &= 3 \times 1 \times c \
\frac{dJ}{dc} &= 3 \times 1 \times b
\end{align*}
$$
为什么要算反向传播?
因为要计算梯度。
实战演示:
接下来尝试计算一个简单结构的梯度,问题描述如下:
假设我们的基础模型就是y = wx+b,其中w和b均为参数,我们使用y = 3x+0.8来构造数据x、y,所以最后通过模型应该能够得出w和b应该分别接近3和0.8。
简单的来说就是拟合出满足y = 3x+0.8这个曲线。
步骤分为四步:
# 1 构造数据
# 2 设计正向传播 和 反向传播函数 来训练网络
# 3 训练
# 4 画图画出拟合出来的曲线
过程如下图:
从左向右是正向传播部分
从右向左是反向传播部分
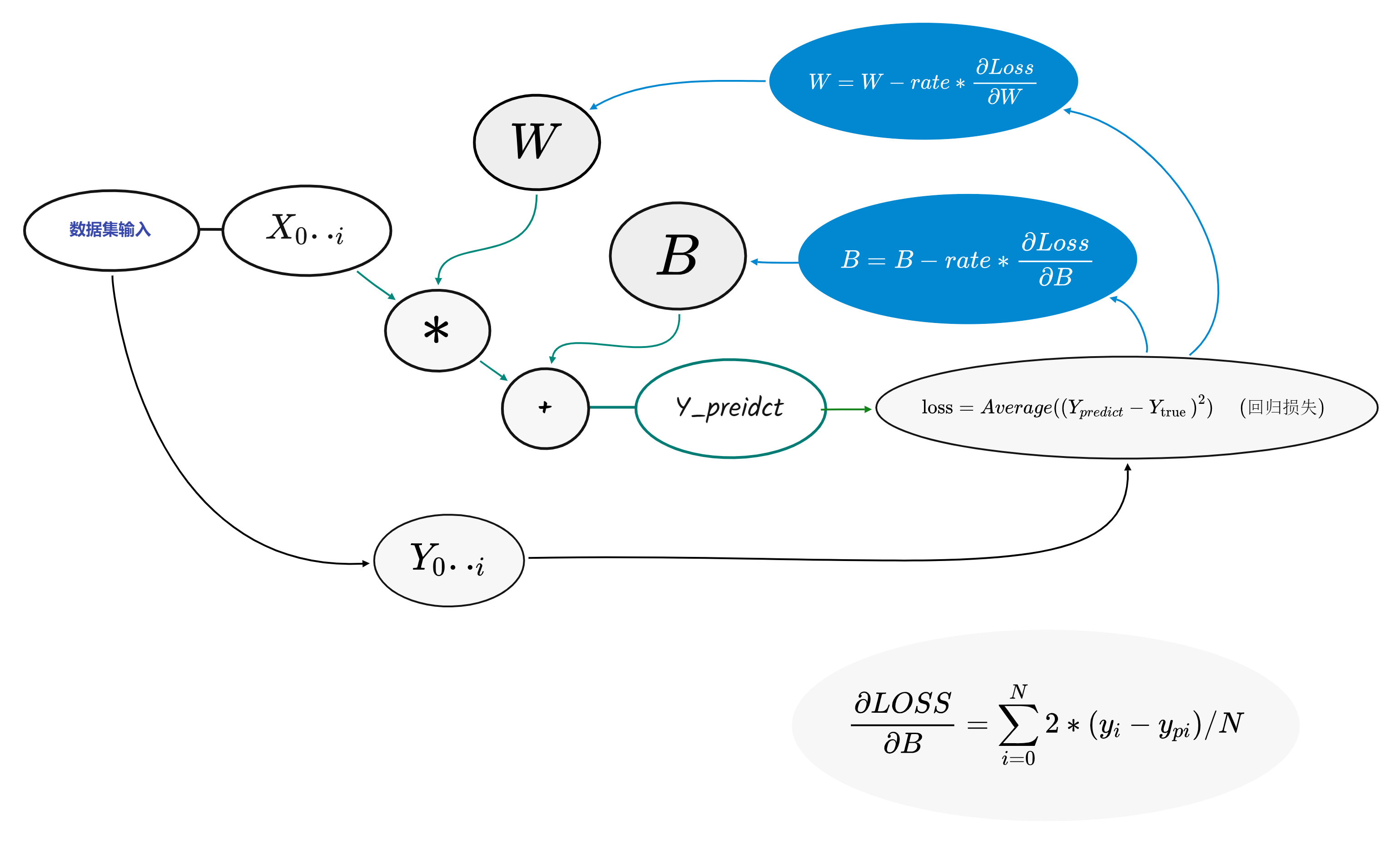
对于W和B其计算类似这里单独说B即可
对于B的梯度满足下式,值得注意的是这里的Loos求取的是平均值实际上出来的是一个标量,对于标量的梯度计算实际上也是一个平均值(这里值得思考一下)。
$$
\frac{\partial Loss}{\partial B} = \sum_{i=0}^N 2*(y_i-y_{pi})/N
$$
反向传播后对B进行梯度下降:
$$
B = B - rate *\frac{\partial Loss}{\partial B}
$$
梯度下降以后再次进行正向传播即可,计算出来Y_p,最后计算出来Loss。
正向传播满足下式:
$$
Y_{predict (0…N)} =X_{predict (0…N)}* W + B
$$
代码如下:
import torch
import numpy as np
import matplotlib.pyplot as plt
# 1 构造数据
x_number = 50
x = torch.rand([x_number, 1])
y = 3 * x + 0.8
rate = 0.01
study_time = 3000
# 2 正向传播 和 反向传播
w = torch.rand([1, 1], requires_grad=True, dtype=torch.float32)
b = torch.rand(1, requires_grad=True, dtype=torch.float32)
y_preidct = torch.matmul(x, w) + b
def forward_propagation():
global x, w, b, y_preidct
y_preidct = torch.matmul(x, w) + b
# 计算 loss
loss = (y - y_preidct).pow(2).mean()
return loss
def back_propagation():
global x, w, b, loss, rate, y_preidct
test = 0.0
if w.grad is not None:
w.grad.data.zero_()
if b.grad is not None:
b.grad.data.zero_()
# 反向传播
loss.backward()
w.data -= w.grad * rate
b.data -= b.grad * rate
#此处为了验证b的梯度进行计算
# for j in range(x_number):
# test += ((y[j] -y_preidct[j].item()) * 2)
# print("b:", b.grad)
# print("b_t:", test/x_number)
# 3 训练部分
for i in range(study_time):
loss = forward_propagation()
back_propagation()
if i % 10 == 0:
print("w,b,loss", w.item(), b.item(), loss.item())
# 4 画图部分
predict = x * w + b # 使用训练后的w和b计算预测值
plt.scatter(x.data, y.data, c="r")
plt.plot(x.data.numpy(), predict.data.numpy())
plt.show()
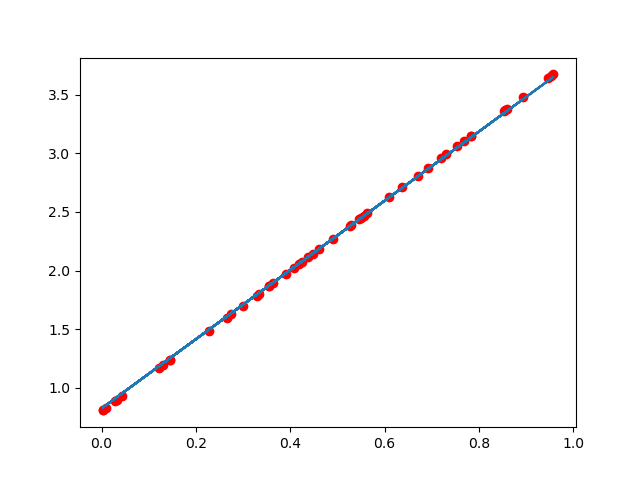
红色的是数据集结果蓝色是训练出来的结果:
当训练次数比较少的时候拟合曲线不正确:
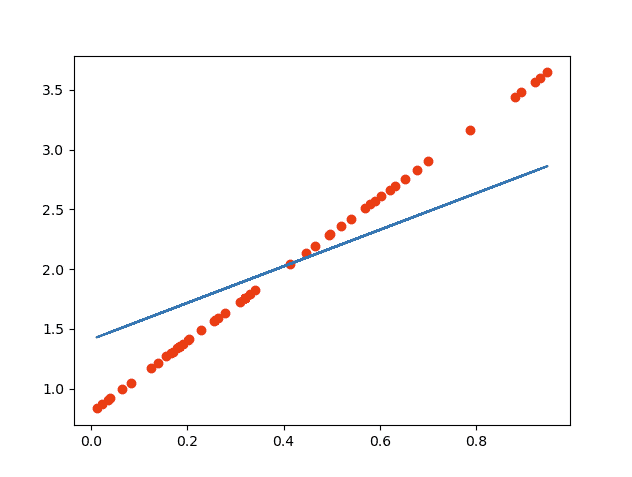
当把学习率降低(变化范围减小),增加学习次数就可以得到很好的结果:
参考文献: